Advanced Modal Logic

高级模态逻辑 （2025 春季） Advanced Modal Logic  (关于钻石与盒子的故事)
教师：王彦晶， 时间：每周二 3-4节 周四 3-4节 地点：文史楼 203

其他相关课程请见: https://logic.pku.edu.cn/quicklinks/539606.htm

News

Lecture 8（Slides, 3月14日) 我们讲了滤模型的定义，这是一种“有损压缩”。过滤模型定义的是一类模型，对关系提出了两个要求，凡是满足这两个要求的关系都可以构成过滤模型中的关系，因而基于一个给定的模型和一个公式（看成子公式封闭的公式集）我们可以有多个滤模型。注意在涉及等价类的定义中，要证明代表元的选取不会影响定义。另外，语言中初始符号的选择会影响定义和证明，要小心（见补充材料）。之后，我们引入了最后一种重要的模型构造方法：超滤扩张。我们希望可以把一个克里普克模型加一些可能世界变成一个模态逻辑等价的模态饱和模型。但其实我们并不直接加可能世界，而是把可能世界看成极大一致的公式集，而把公式看成可能世界的集合，进而把可能世界看成一些“极大一致”的可能世界集的子集族，这些子集族就是所谓超滤子，会被当成可能世界构造我们的超滤扩张。所以超滤子的一个直观就是可以被看成“潜在公式”的一个极大一致集。特别的，主滤子是那些由一个点生成的超滤子，另外还有一些不是主滤子的超滤子，将在我们的超滤扩张中起到重要作用：他们是增加的可能世界。

补充：

  • 文学锋老师关于 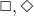\Box, \Diamond 做初始符号的常见问题的文章。
  • 我们遇到的模型检测不可判定但可满足性可判定的逻辑 （注意这里模型检测是在epistemic model上不可判定，在extended model上可判定）
  • 命题逻辑公式可满足性的判定可能是应用最广泛的逻辑学计算问题，有很多工业级的SAT-solver。

Lecture 7（Slides 3月11日）我们开始介绍模型构造和转换的一些办法。我们可以证明通过这些构造得到的新的点模型，使得它和原点模型间是互模拟的，从而证明这些构造不会改变模态公式在特殊点上的真值。利用这些模态公式在这些构造下保持不变的结果，我们可以证明一系列模态不可定义性的结果。最后我们介绍了模型的树展开，并通过对模型的树展开进行深度和广度的“修剪”证明了模态逻辑具有有穷模型性。这种方法有一个缺点：我们通过树展开和修剪枝杈得到的有穷模型未必具有我们希望的性质（从而不见得属于特定模型类）。

Lecture 6（Slides 3月6日) 课上我们总结了bisimilarity与模态等价之间的关系以及与之相对应的各种bisimulation games。希望大家至少能够熟悉Game、自动机或者语义图中的一种方法，会对处理很多逻辑的判定性问题有帮助。我们主要讨论了互模拟和逻辑等价性之间的关系。我们引入了模态深度的概念，证明了当命题变元只有有穷多个，模态词也只有有穷多个的情况下，模态度最大为n的模态公式在逻辑等价的意义上最多有有穷个（用命题逻辑真值表有穷的思路）。利用这个结果我们在有穷多个命题变元的情况下证明了n-互模拟＝ML_n的逻辑等价，继而证明了\omega－互模拟＝模态逻辑等价。我们开始考虑在什么样的情况下，bisimilarity等同于模态的逻辑等价关系。我们首先证明了在像有穷的模型类上，bisimilarity和模态等价是一回事，之后我们要引入了一个比像有穷更一般性的模型性质：模态饱和性。我们证明了在模态饱和模型类上互模拟与模态逻辑等价性是一样的。事实上，m饱和性的定义可以很自然的bridge证明中的gap。它也可以被看成一阶逻辑模型论中的饱和概念在模态逻辑中的应用（以后的课也会谈到）。它的重要性主要体现在之后重要结果的证明中，例如，我们在后面的课将会看到任何一个模型都能被转换成一个与之模态等价的m饱和模型，所以m饱和模型可以被看成普通模型的“理想代表”。之后的作业中会让大家证明m饱和模型类是至少包含它自己的模型类里具有Hennessy–Milner性质的最大的模型类，也就是说它不可能再被扩充了。

补充: 无穷轮的bisimulation也是determined (source: Johan van Benthem, by Gale-Stewart Theorem 这个定理可以参考这个文档)

Lecture 5（Slides, 3月4日）我们首先简述了集合论领域对于互模拟的发现：在非良基的集合论里，集合可以被看成图属于关系看成边，而集合间一个自然的等价关系恰恰是他们对应图的互模拟关系。非良基的集合论可以用来直观地定义无穷的stream和无穷树，对于计算机科学很重要。bisimulation特别适合处理带环的图的等价性。很多带环的图可以体现结构主义的精神：一个点的意义在于其与其他点的关系，比如google的page rank。在结构主义数学基础中也有一派是做Synthetic Math。我们之后从游戏的角度去看互模拟。首先我们引入了比较抽象的 Game 的概念，其实很多逻辑中的概念都可以和游戏建立起比较精确的联系，事实上按照 Hintikka 的说法，逻辑的产生还和 Game 有渊源：是亚里士多德在给柏拉图学院编制对话游戏的手册的时候发现有些话之间有很有意思的关联，说了一句之后，后面有些话就不能说了，否则感觉就矛盾了，这起发了他的三段论的工作。我们讨论了二人有穷深确定性完美信息胜负游戏的判定性定理的证明。可以通过自下而上的标记或逻辑公式的否定（及排中律）来证明游戏双方中肯定有一个人有必胜策略。我们还举例说明了“二人”、“确定性”以及“完美信息”条件的重要性，并与Hintikka的Independence friendly logic（IF-logic）做了联系：IF-logic里的公式可能包含不受前面量词辖域限制的量词，这些公式的语义恰恰是通过不完美信息的博弈给出的。我们还讨论判定性定理在国际象棋上的应用。之后我们证明了互模拟和互模拟游戏中Defender存在winning strategy的对应关系。n-互模拟对应n轮的互模拟游戏，\omega-互模拟对应任意有穷轮的互模拟游戏，标准互模拟对应无穷多轮的互模拟游戏。特别的，游戏的角度是有一些特点的，比如要证两个模型不是互模拟的我们只需要找到一个 spoiler 的winning strategy 即可，按照原始定义的话，要说明任何的 bisimulation 都不 work。 注意，winning strategy按定义是函数，很多时候从bisimulation找winning strategy 要保证这样的函数存在而需要选择公理，比如一个点有无穷多后继，spoiler选择其中任何一个，defender都要对上一个点，但是这样能对上的点也可能有无穷多个，所以是在无穷多个里挑一个而且要挑无穷多次。

延伸阅读: Dependence Logic

Lecture 4（Slides, 2月 27日）课上我们回顾了互模拟在模态逻辑里的发现过程，研究了它的定义，指出了一个看似简单的替代定义是循环的。我们强调了互模拟的局部性，余归纳性的特点。粗略地说归纳定义的特点是要找满足特定不等式（封闭条件）最小的解，可以从最小的集合构造；而余归纳是要找满足特定条件最大的解，可以从最大的集合“破坏”得到（不断剔除不属于的）。同时余归纳的定义一个集合可以通过归纳定义其补集实现（因而叫余归纳）。一个模型中的互模拟等价关系（Bisimilarity）可以被看成某个作用在二元关系上的函数f的最大不动点，由Knaster-Tarski定理保证这样的最大不动点存在，可以通过函数从全集开始的超穷迭代得到（Kleene不动点定理保证）。这也给了我们一个在有穷模型中找互模拟等价关系一个办法：从全关系开始进行有穷次迭代总能找到那个最大不动点。每个互模拟关系R都是不等式R包含于f(R)的一个解，而互模拟等价恰是那个最大的解。从不动点的角度看互模拟也是计算机界之所以能发现互模拟的原因。标准的互模拟不能用简单的归纳方式定义，不过我们可以用n－互模拟逼近标准的互模拟（不过所有n－互模拟等价的交并非就是互模拟）。

延伸阅读(包含本课讲的不动点的内容)：

D. Sangiorgi, On the origins of Bisimulation and Coinduction. ACM Transactions on Programming Languages and Systems, Vol.31, No.4, 2009. 

这几节课的内容基本上在教材上没有，还请大家看老师给的参考文献。另外，也请大家及时阅读教材里涉及模态逻辑语义以及 bisimulation 的章节。

Lecture 3 （Slides, 2 月 25 日) 课上我们先回顾了上节课的内容，之后定义了模态公式的点模型可满足，模型全局可满足，点框架有效，框架有效的概念（按模型／框架，局部／全局分四种情况）。我们考虑模型间等价关系的两种定义方式：1 通过模型间的结构关系定义 2 通过某种逻辑下的等价关系定义：两个模型被视作等价如果他们不能被某种逻辑中的公式区分（即不存在一个该逻辑的公式在这两个模型上分别为真和假）。对于模型间的每种结构等价关系我们希望通过某种逻辑的等价性来刻画。我们解释了为什么希望要有刻画的结果：1. 如果先有一个逻辑，可以试图用一个结构等价关系刻画其逻辑等价关系，从而对这个逻辑的区分能力（甚至表达能力）有更清楚的认识。2. 如果先有一个结构等价关系，可以试图用一个逻辑等价关系来刻画这个结构等价关系，从而能更清楚的看到这个结构等价有什么意义：什么样的性质（用逻辑语言表达）能在这个结构等价关系下得到保持。

之后我们看了一些简单例子，比如考虑有多个一元模态词(\Box_a,\Box_b,\Box_c,…)的语言，每个模态词\Box_x在模型中对应关系R_x. 我们可以定义trace等价：看两个点模型里能走出来的路（abc这种有穷序列,…）是否一样. 这个结构等价关系，对应的是模态逻辑的一个小片段，里面只有\Diamond_x \Diamond_y…\Diamond_z \top 这种公式。之后我们接着看一些更复杂一点的例子。课上这些例子来源于进程代数，在那里研究者关心的是各种进程（可简单理解成程序）表现出来的行为 (behavior) 即能观察到的表现。根据不同的可观测能力，进程之间可以定义有不同的等价关系，可以用模态逻辑进行刻画。我们举了一个例子，说明在证明逻辑等价刻画结构等价的时候，对公式作结构归纳证明是最自然的，但是这时要注意应用归纳假设的条件是否适用（回忆课上的例子，可称为“\omega-手观音”大战“如来佛”）。

关于structural equivalence在理论计算机中应用的延伸阅读：
R. J. van Glabbeek The linear time – branching time spectrum CONCUR ’90 Lecture Notes in Computer Science, 1990, Volume 458/1990, 278-297

Lecture 2（Slides 2月20日）课上我们回顾了克里普克语义。注意：克里普克模型里面的点可以有多种解释，不同的解释可能会带来技术上的不同发展与限制；零元模态词可以对应框架世界集的一个子集；模态语言的similarity type给出的是逻辑符号，不像一阶逻辑的字母表是非逻辑符号；克里普克模型中每个点的意义来源于上面成立的基本命题变元以及这个点和其他点的关系；注意多元模态词的定义中的量词，为什么要这么定义？我们还给出了全局模型检测的labelling方法。

补充材料：

  • 关于模型检测 (Model Checking)
  • 宇宙的原子个数
  • 初始符号用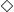\Diamond还是\Box 在证明系统那里是有区别的，可参考文学峰老师的文章，等讲到后面再细讲。
  • Montague 证明通常的模态词不能用谓词表示的工作: Montague, R. (1963). Syntactical treatments of modality, with corollaries on reflexion principles and finite axiomatizability. Acta Philosophica Fennica, 16, 153–167 这文章不好找到，可以看这里Thomason的文章: A Note on Syntactical Treatments of Modality Synthese, Vol. 44, No. 3 (Jul., 1980), pp. 391-395
  • Worlds vs. Possibilities/states的早期文章

关于可能世界语义起源的文章可见（请自己试图找到文章的pdf）：

  • B. Jack Copeland: The Genesis of Possible Worlds Semantics. J. Philosophical Logic 31(2): 99-137 (2002)
  • Max Cresswell: Modal Logic before Kripke. Organon F 26(3),(2019)
  • B. Jack Copeland: Meredith, Prior, and the History of Possible Worlds Semantics. Synthese 150(3): 373-397 (2006)

Lecture 1（Slides1，Slides2，2月18日）在课程介绍之后，我们从对模态逻辑的不同描述出发，试图从不同角度认识模态逻辑：模态逻辑作为非经典逻辑起源于C刘对于严格蕴含的讨论，由此引出“可能”与“必然”，最重要的特点是把本来在元语言里的概念拿到对象语言里谈；模态逻辑作为一个领域是关于各种模态词的逻辑的总称；命题模态逻辑的语言是通过命题逻辑语言加上各种模态算子得到的；模态逻辑在克里普克语义下是讨论关系模型／框架性质的逻辑；模态逻辑在模型类定义能力的意义上是一阶逻辑的一个片段，在框架类定义能力的意义上是（一元）二阶逻辑（MSO）的一个片段；最后模态逻辑的可满足性问题是可判定的。在本课中，我们通常是从（抽象）模型论的角度谈论具体的逻辑，一个逻辑指的是一个三元组<逻辑语言，模型类，可满足关系>。基本模态逻辑即为<命题模态逻辑语言，关系模型类，克里普克语义>。它具有如下三方面的优点：1. 关于模态词的语言简单直观，2. 关系模型应用范围广泛，3. 在克里普克语义下模态逻辑是一阶逻辑的一个性质良好的片段（就模型可定义性而言）：紧致性，有穷模型性，互模拟下的不变性，以及可判定性等等。正是基于这些优点，模态逻辑较好的平衡了语言的表达力和复杂性，在诸多不同领域里发挥了很大的作用。我们将对模态逻辑的这些良好性质进行细致的讨论。

注：本节课仅仅作为一个导言，如果对上述诸多名词概念不是很清楚请不必担心，我们将在后面的课程中放慢速度，仔细讲解。

补充：

大概内容（Contents）： 


基础理论：模型与框架，正规模态逻辑，典范模型与完全性；表达力与不变性：互模拟，对应理论；有穷模型性与可判定性；代数语义学：表示定理，模态代数与一般框架；


(若有时间) 邻域语义学，非经典逻辑的克里普克语义, 一阶模态逻辑，模态逻辑的一些应用，模态逻辑与自动机的对应等。

本课的主题是模态逻辑, 但是也会介绍很多适用于逻辑学各种分支的问题和技术想法。 无论你是否上过模态逻辑课或是否用过本课的教材，相信本课能带给你一些新的东西. 课堂上有一小半的内容不在教材上, 由教师补充。

目标（Objectives）：


知识储备：知道模态逻辑的基本结果和重要定理的证明策略。 
逻辑技能：对新的模态逻辑知道问什么问题并能解决一些，至少对问题难易程度及关键点有正确评估。 
学术技能：熟练阅读英文教材及文献，能用\LaTeX写作业做slides，能独立清晰地做学术报告。 
态度培养：一种看各种问题的“模态视角”，不畏惧复杂问题，愿意用逻辑工具形式化地分析问题，对学术问题具有较开放的心态。 

教材（Course material）：

P. Blackburn, M. de Rijke and Y. Venema. Modal Logic, Cambridge University Press, 2001 

参考书：
Handbook of Modal Logic, P. Blackburn, J. van Benthem, F. Wolter Eds. Elsevier, 2006 
J. van Benthem. Modal Logic for Open Minds, CSLI Publications, 2010
R. Girle. Modal Logics and Philosophy (2 ed.), McGill-Queen’s, 2010
周北海，《模态逻辑导论》，北京大学出版社，1996
文学锋，《模态逻辑教程》，科学出版社，2021
Boxes and Diamonds: An Open Introduction to Modal Logic,  Remixed by Richard Zach, 2020

考核（Grading）：
1. 作业（80%） ：原则上两周一次，用\LaTeX写，挑成绩最好的n-1次取平均分计入总成绩（n\leq 7）。
2. 当堂学术报告（20%）：补充内容

大致安排（Plan）：
第一周至十五周老师讲 (5 月 6 号停课一次)，第十六周同学分组报告

预备知识（Prerequisites）：
命题逻辑及一阶逻辑基本知识，模态逻辑的基础知识。

Office hours：
周四课后办公室2139，请提前预约。

意见、建议或其它问题请发email：y.wang艾特pku.edu.cn